En un artículo anterior presentamos las particularidades de un fenómeno conocido como golpe de ariete que se produce en las redes hidráulicas en general, y las de los parques acuáticos en particular. En esta nueva investigación sobre el mismo fenómeno, diferenciaremos entre golpe de ariete rápido o lento, según el tiempo de cierre de la válvula de corte, y presentaremos diversas formulaciones para el cálculo de la sobrepresión asociada a cada uno de estos tipos. Por último, expondremos los casos concretos en los que se produce el golpe de ariete en las instalaciones hidráulicas de los parques acuáticos, y las medidas disponibles para mitigarlo.

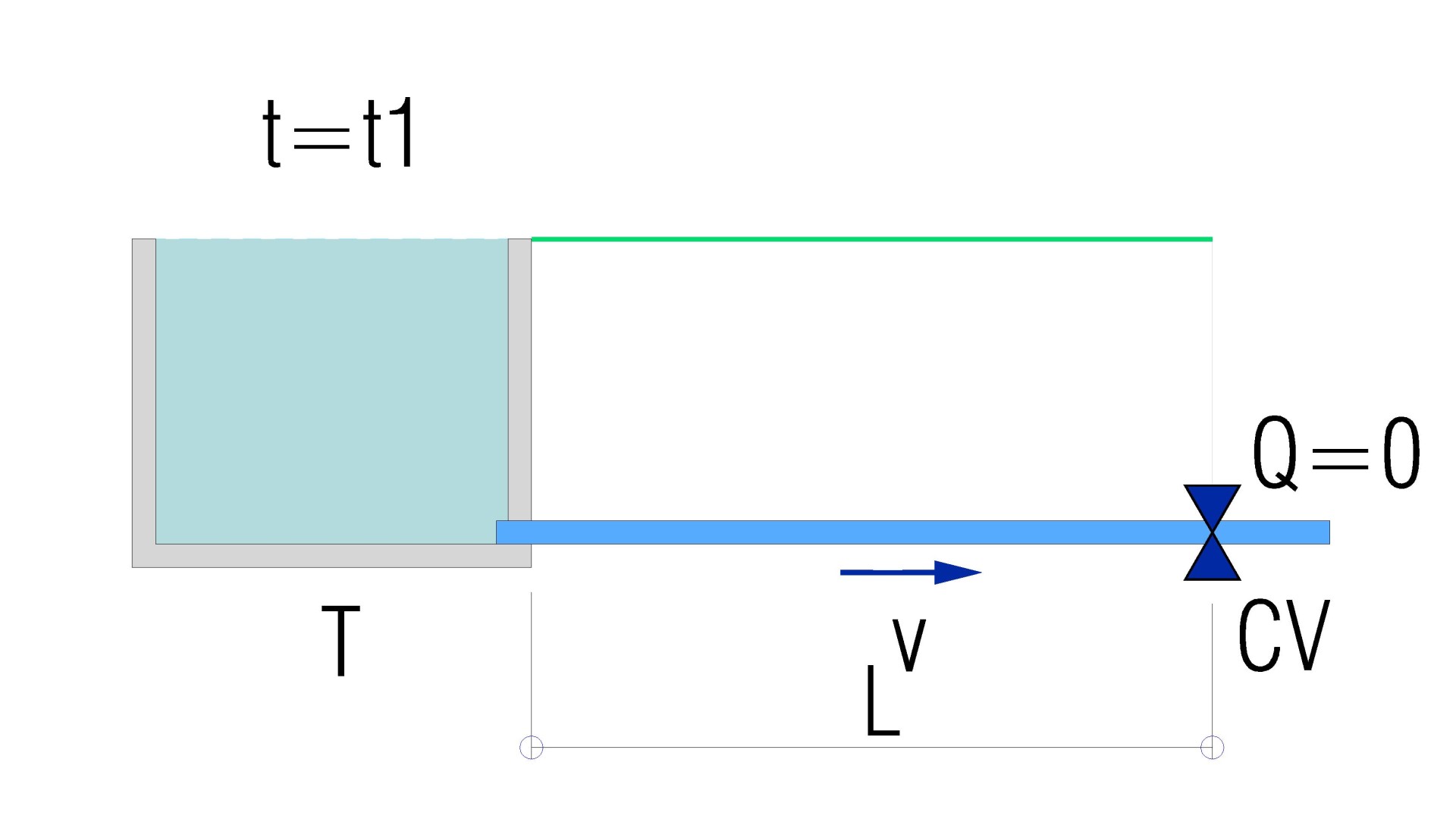
En el contexto del mismo ejemplo que utilizamos en el artículo anterior, determinamos que el tiempo de cierre (Tc) corresponde a la duración de la maniobra de corte de flujo en la tubería. Asimismo, al tiempo que tarda la onda de sobrepresión (de velocidad a) en recorrer la tubería (de longitud L), desde la válvula de corte (CV) hasta el depósito (T), la llamaremos L/a. En consecuencia, la onda reflejada desde el depósito alcanzará la válvula en un tiempo 2·L/a.

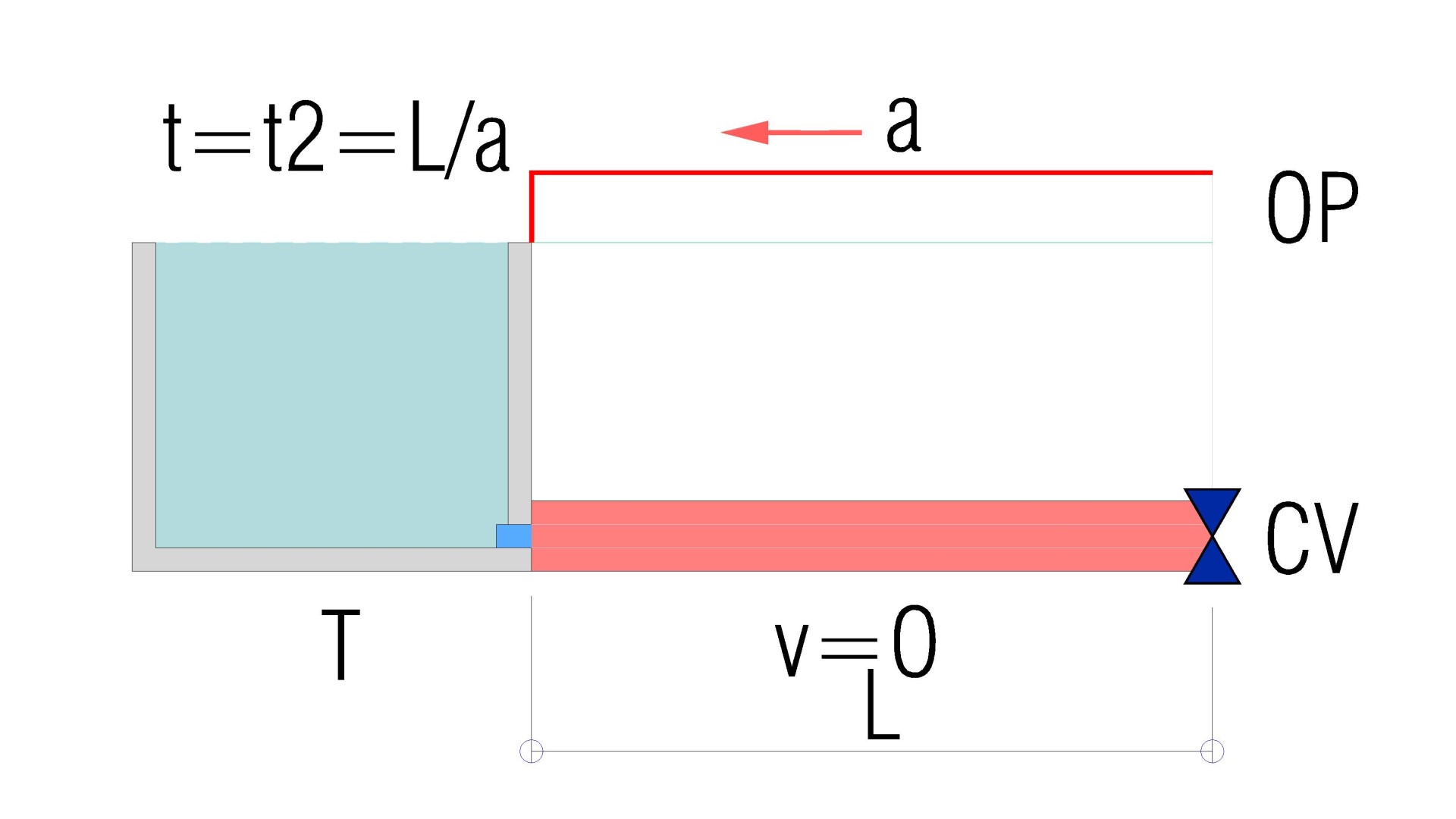
En la imagen se aprecia el instante t2 = L/a, momento en que la onda de sobrepresión alcanza el depósito.

Acto seguido la onda de presión se refleja y vuelve hacia la válvula de corte.

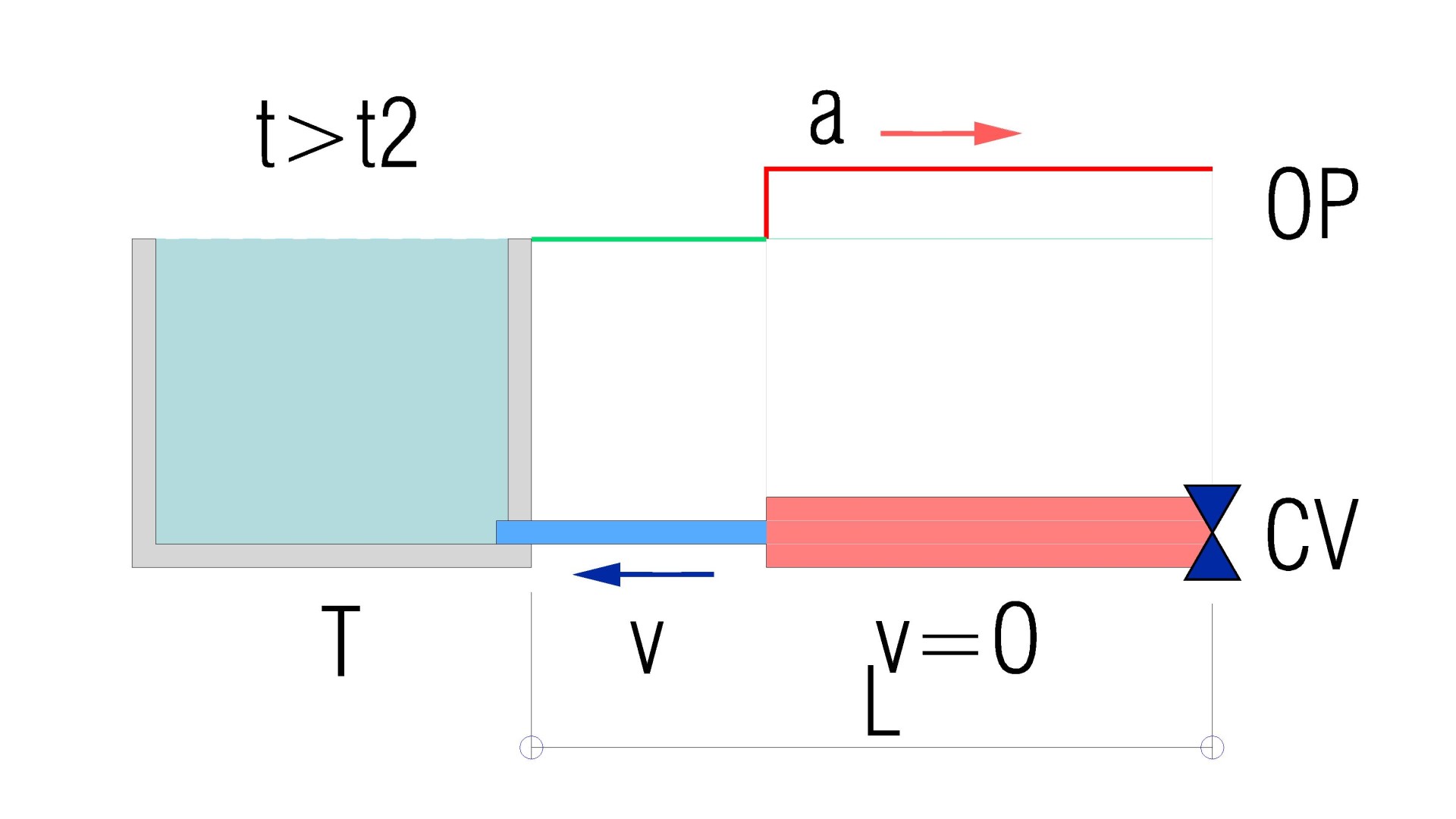
Así, pues, es en el instante t3 = 2·L/a, cuando la onda de presión alcanza la válvula de corte.

Cuando el cierre es rápido o, dicho de otra forma, Tc < 2·L/a, la onda de sobrepresión alcanza la válvula cuando ya está completamente cerrada. En este caso, la sobrepresión (OP), se calcula con la fórmula de Allievi, así:

OP = a·v/g

Donde:

a: velocidad de la onda

v: velocidad del fluido

g: aceleración de la gravedad

Así, en los cierres rápidos, la sobrepresión es independiente del tiempo de cierre, y es equivalente a la que se produciría si el cierre fuera instantáneo, o Tc ≈ 0.

Cuando el cierre es lento, o Tc > 2·L/a: en este caso, la onda de sobrepresión alcanza la válvula cuando aún no se ha cerrado por completo, lo que favorece que una parte de esta sobrepresión se alivie. En esta situación, la sobrepresión se calcula con la fórmula de Michaud:

OP = 2·L·v/(g·Tc)

Como puede apreciarse, en el cierre lento, la sobrepresión es inversamente proporcional al tiempo de cierre de la válvula. Así pues, a mayor tiempo de cierre, menor sobrepresión en la tubería por golpe de ariete.

Las instalaciones hidráulicas de los parques acuáticos, con grandes grupos de impulsión desde los que se bombea agua a los toboganes acuáticos y demás atracciones, pueden sufrir golpe de ariete durante la maniobra de parada de las bombas. En ese caso, se produce un frente de onda de presión negativa y, en consecuencia, el golpe de ariete se desencadena en su fase inversa. Para mitigar este efecto, debe garantizarse que el tiempo de parada de la bomba (equivalente al tiempo de cierre de válvula, o Tc, anteriormente descrito) es mayor que el tiempo de recorrido de la onda de presión 2·L/a. Nos encontraremos así en la opción de cierre lento (parada lenta de la bomba) y, por tanto, la sobrepresión producida en la tubería será ostensiblemente menor. Huelga decir que, cuanto más lenta sea esa parada, menor será la sobrepresión.

En la práctica, para evitar el golpe de ariete, es habitual que las bombas se instalen en los parques acuáticos con variadores de frecuencia o arrancadores suaves. Estos dispositivos garantizan precisamente una maniobra de parada de las bombas lo suficientemente lenta como para que la sobrepresión producida en la tubería sea despreciable.

Por Luis Llor, ingeniero hidráulico sénior en el Dpto. de Arquitectura de Amusement Logic