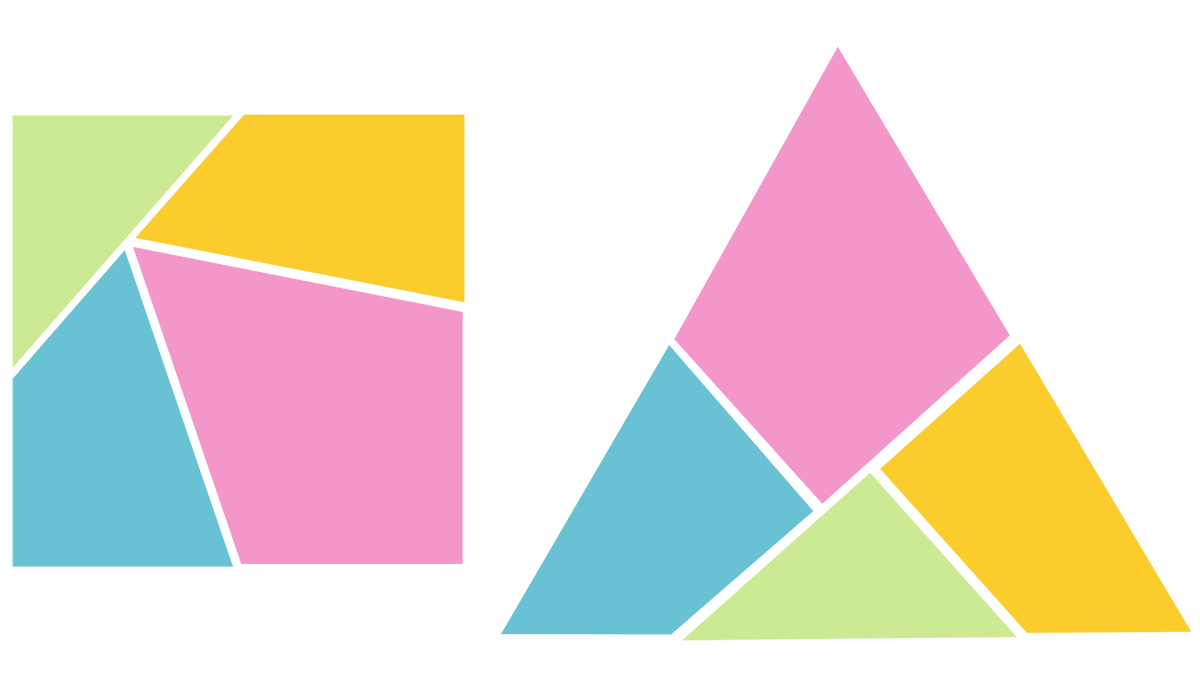En 1902, el matemático inglés Henry Ernest Dudeney (1857-1930) planteó en su columna de pasatiempos, en el dominical Weekly Dispatch —conocido como Sunday Dispatch de 1928 a 1961, año en que se fusionó con el Sunday Express— un desafío simple en apariencia, pero que escondía una complejidad fascinante: ¿cómo dividir un triángulo equilátero en la menor cantidad posible de piezas de tal forma que, al reordenarlas (solo mediante traslación y rotación, sin superposición), formen un cuadrado perfecto?

Un lector llamado Charles William McElroy propuso una ingeniosa solución con solo cuatro piezas conectadas por sus vértices y articuladas, una suerte de rompecabezas mecánico que permitía, con un simple giro, transformar el triángulo en un cuadrado. Durante los últimos 122 años, nadie logró el mismo resultado con menos de cuatro piezas, aunque nunca existió por lo demás indicio alguno de que pudiera lograrse.

Si había dudas, se desvanecieron en diciembre de 2024, cuando los matemáticos Tonan Kamata y Ryuhei Uehara, del Instituto Avanzado de Ciencia y Tecnología de Japón, y Erik D. Demaine, del Massachusetts Institute of Technology de Estados Unidos, demostraron que no es posible resolver la cuestión con menos de cuatro piezas. Por tanto, la que dieron McElroy y Dudeney hace más de un siglo es «óptima» —o, dicho de otra forma, es imposible una solución más eficiente.

Para resolver el enigma geométrico, Kamata y sus colegas matemáticos lo redujeron a un problema de teoría de grafos. De esa manera, en lugar de intentar infinitas combinaciones de cortes geométricos, delimitaron el problema a uno de análisis de las posibles disecciones como posibles grafos. Por cierto, un grafo es una estructura matemática formada por vértices —también conocidos como nodos o puntos—, conectados por aristas —llamadas asimismo arcos, enlaces o líneas. La teoría de grafos es pues la parte de las matemáticas que estudia los grafos. Pero volvamos al acertijo geométrico: efectivamente, cada corte del triángulo equilátero inicial se representa como una arista y cada punto de intersección como un vértice. Con ello, consiguieron clasificar todas las variaciones posibles en categorías manejables, y redujeron un problema infinito a un conjunto finito de casos. El resultado ya lo conocéis.

Más allá de su valor teórico, este descubrimiento tiene implicaciones en campos tan diversos como el diseño, la arquitectura e incluso la pedagogía matemática. Por citar solo un ejemplo, el estudio de diseño y arquitectura londinense DHaus trasladó el puzzle de Dudeney —también conocido como la «disección de Dudeney» o el «problema del mercero», este último apelativo por la presentación que el propio Dudeney le dio como acertijo nº 26, en The Canterbury Puzzles (1907), en la forma del desafío que un mercero lanza a sus interlocutores, el de cortar una pieza de tela con forma de triángulo equilátero para formar ese cuadrado perfecto—; el estudio DHaus, decíamos, trasladó ese juego geométrico al diseño de una mesa y de una casa con partes móviles.

Ya veis, problemas aparentemente simples pueden esconder profundidades insospechadas. En cualquier caso, la próxima vez que veáis un triángulo o un cuadrado, quizá recordéis que, detrás de su forma aparentemente estática, se esconden conexiones inesperadas, transformaciones sorprendentes y, sobre todo, la elegancia eterna de las matemáticas.

Fuentes: Arxiv.org, Scientific American, Wolfram MathWorld, Gutenberg.org, Wikipedia.
Imágenes: DHaus 1, DHaus 2, Wikipedia.